IntroductionThis paper explains why and how atmospheric pressure decreases with altitude and discusses the variations in oxygen (O2) level that affect aerobic efficiency. It is written mainly for runners of the Pikes Peak Ascent and Marathon but it applies to most any altitude race. The perspective is that of a meteorologist so the physiological processes of respiration are not covered here. What is covered are the answers to two specific questions:
Answer to Question #1We are very lucky to have an atmosphere to breathe. That may seem like a silly thing to say because we would of course not even be here if it weren’t for the atmosphere. However, most people do not realize how tenuous the earth’s atmosphere really is. In the big picture, the gases that surround our planet are just a wispy little film. Given a model of the earth the size of a car, the atmosphere would be only ½ inch thick.Another thing to consider is that since a vacuum surrounds our planet, why doesn’t the atmosphere just go fizzing out into space? The reason is that gas, even though we can’t see it, is matter just like Newton’s apple and is likewise pulled toward the earth. Unlike Newton’s apple, the gas is also very compressible. So why then doesn’t it squish down to a super dense layer at our feet? Balance is the key to this puzzle just like many things in nature. The gas is fighting to go fill the void in space but the earth says “I don’t think so” and thus a compromise is established, again lucky for us. The technical term for this compromise is the hydrostatic balance, which is a simple little equation with critical consequences for high altitude runners:
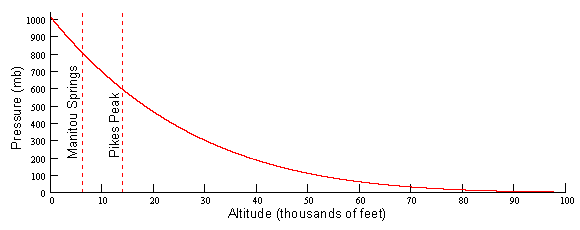
which states that the rate of change of pressure (p) with respect to altitude (z) equals the negative of the density (r) times the gravitational constant (g). The negative sign tells us that the pressure decreases with altitude which means that the density must also decrease. Since the rate of pressure decrease is directly proportional to the density, there must be slower rate of decreasing pressure the higher up you go. This is known as an exponential decay. One curious result of this is that there is no real “top” to the atmosphere. It just slowly tapers off to infinity. We can solve the hydrostatic balance equation for pressure as a function of altitude and plot it as in Figure 1. Notice that the curve starts off very steep near the surface (rapid rate of decreasing pressure with height) and steadily becomes more shallow (slow rate of decreasing pressure with height). The consequence of this for runners of Pikes Peak is that for running in the steep portion of this curve, the atmospheric pressure (and thus the amount of available oxygen) drops off rapidly with height.
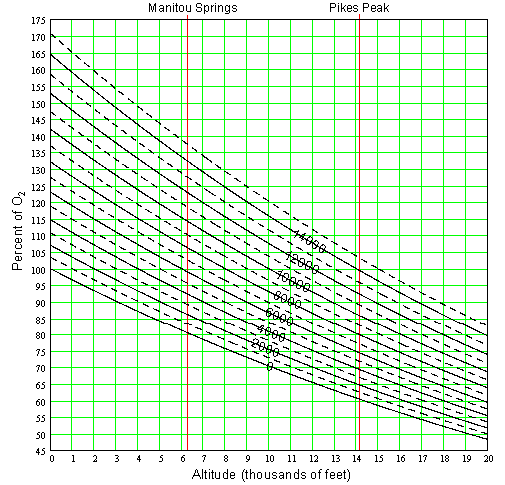
The lowest 60 miles of the atmosphere is very well mixed and thus maintains roughly the same proportions of the different gasses is consists of. O2 is actually only a bit more than one fifth (21% by volume, 23.14% by mass) of the atmospheric gas. (Most of what you breath, 78% by volume, 75.51% by mass, is nitrogen.) Since the O2 part of the atmospheric pressure is constant, we can simply equate the percent decrease in total pressure to the percent decrease in O2. For example, from 1000 mb to 500 mb the pressure decreases by ½. The O2 partial pressure (pressure exerted by O2 portion of the gas) decreases from 231.4 mb (23.14% of 1000 mb) to 115.7 mb (23.14% of 500 mb), a reduction of ½ just like the total pressure. Runners like to know the percent decease in O2 which can get confusing because it is a relative thing. At any given altitude, all runners will of course experience the same absolute O2 partial pressure but the percent decrease is based on a reference altitude. The term reference altitude is defined here as the elevation of the place you live and spend the majority of your time. This is where the O2 level is at 100% for you since it is what your body is accustomed to. An increase in altitude from your reference altitude, decreases the O2 from that 100% and visa versa. Figure 2 can be used to figure percent O2 at another altitude for a given reference altitude.
For example, say your reference altitude is in Colorado Springs at 6,000'. To find the percent of this particular 100% O2 level at the top of Pikes Peak, first locate the diagonal curve for 6,000' in Figure 2. Now follow it down to the right to the intersection of the 14,110' altitude, then read off the percent O2 (about 74%) on the left. This result comes from the fact that the O2 partial pressure at the top of Pikes Peak is 141.6 mb, which is 74% of 190.1 mb (the O2 at the reference altitude). Now let’s say you are from Houston at sea level (0 ft). Figure 2 shows that Pikes Peak would have 61% of the O2 you are conditioned to. Do you see any advantage to living at a higher altitude?
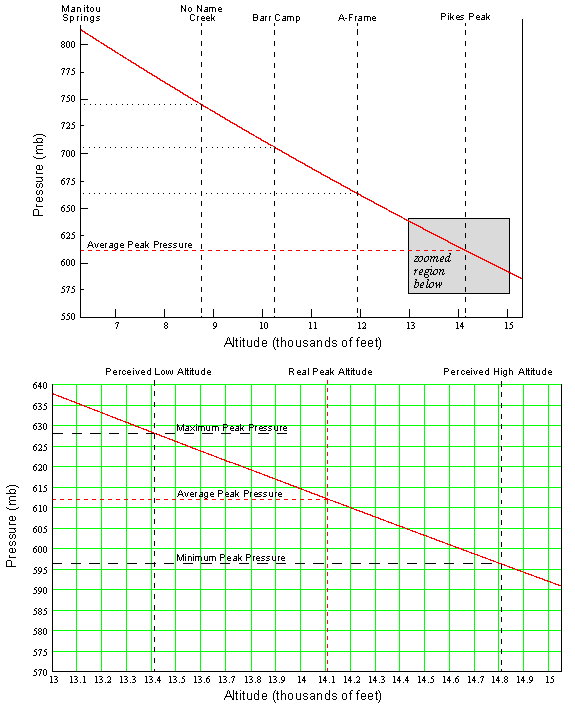
Answer to Question #2Now that you understand more about pressure variation with height, we can address the second focus question of this paper which deals with horizontal pressure variations. The atmosphere stays close to Figure 1 but sloshes all around creating horizontal pressure differences on big scales (HIGHS and LOWS you see on weather reports) and small scales (such as a thunderstorm). So as the pressure changes at any point, the amount of O2 is of course going to change. Normally, this fluctuation is imperceptible but if you are already in a decreased O2 environment, as up on Pikes Peak, you will feel the difference. In general during a high pressure it will feel like you are running at a lower altitude and during a low pressure it will feel like you are running at a higher altitude.The average summertime pressure on top of Pikes Peak is 612.0 mb. On the large scale, the pressure typically varies about ±12 mb and for small scale about ±4 mb. Therefore the extreme range of possible pressures on the Peak during the summer is ±16 mb or 596 mb to 628 mb. Using the graph in Figure 3, the lower pressure gives an equivalent altitude of 14,810' and the higher pressure equates to 13,410'. This means that during your summer training on the Peak, it is possible to have a 1,400' swing in the equivalent altitude. Do you see why things can feel so much different depending on the day?
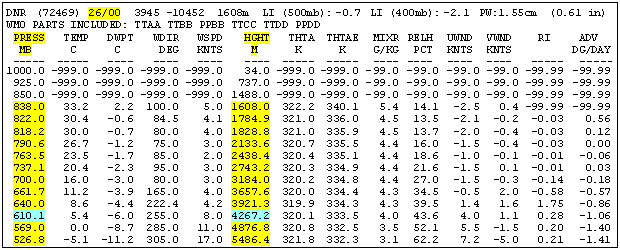
Forecast and ObservationThe forecast variation of pressure on Pikes Peak is not something you are likely to get on a typical weather report. So how can you know in advance or during your run on the mountain if it is a high or low O2 day?For forecasting the large scale pressure pattern, there is a wealth of information available on the world wide web. Unfortunately, most of it takes a meteorologist to digest. However, you can check out the latest upper atmospheric observation from a nearby location. Since the high altitude pressure pattern changes slowly, knowing the current pressure will normally give you a ballpark prediction for tomorrow. Upper atmospheric observations are made with weather balloons in Denver and Grand Junction at 6 AM and 6 PM daily. One web site that displays the data is http://dweb.met.fsu.edu/index.pl/wxdata/textwx. For the Bulletin type select upperair decoded. In the Station box enter either DNR for Denver or GJT for Grand Junction. For the Time select latest or go back in multiples of 12 hours if needed. After hitting Submit you will get something like Figure 4.
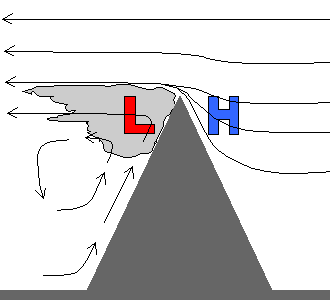
A barometer watch is an expensive toy so there are some rules of thumb you can use as well. In a mountainous environment, the small scale pressure patterns (as well as the weather in general) can vary rapidly. Heating and wind patterns create all sorts of small low and high pressure anomalies. High winds is therefore one clue that something abnormal is occurring. In general, a windy day means below normal pressure since a large scale storm is likely nearby plus small scale eddies with even lower pressure may form on the Peak. Another rule of thumb deals with clouds. Very high, smooth clouds above the Peak will generaly mean above normal pressure since the atmosphere is very stable. Where clouds form on and against the Peak, you can generally expect pressure lower then normal. This can happen in a number of ways. As just one example, Figure 5 shows what happens when a strong, uniform wind blows up against a peak. A “banner cloud” forms in the downstream eddy where the pressure drops several mb. This type of effect, as well as more complex ones, are often observed on Pikes Peak.
ConclusionsA mountain trail runner should understand the normal rate of O2 decrease with altitude and that this rate can vary. A slow day at high altitude can often be contributed to a lower then normal pressure. Being aware of how much O2 is available should help proper pacing.
AcknowledgmentsI would like to thank Nolan Duskin from the Colorado Climate Center for providing historical data on atmospheric pressure on top of Pikes Peak. Thanks also to Matt Carpenter for suggesting this paper and for all the support, advice, and encouragement he has provided to aspiring trail runners.
Numbers, Tools and LinksThe concepts above and the calculators below are based on the hydrostatic equation using a “standard atmosphere” designed for average summer conditions at Pikes Peak:
(Note: If you are not interested in knowing the exact percent O2 and perceived altitude for the current conditions, you can simply use the standard values of 1011.0 mb for station pressure and 0' for station altitude. The resulting percent O2 will be for the average conditions and the perceived altitude will of course match the true altitude.) If you go with the weather report option, it is important to know that the reported barometric pressure typically is not station pressure but actually the equivalent sea level pressure (ESLP). This is a trick forecasters do to aid in surface weather analysis. ESLP is the station pressure increased (by an amount based on the principles discussed above) to a value that equates it to a common reference altitude, chosen to be sea level. That is why the Colorado Springs weather report might say the barometric pressure is 29.85 "hg which sounds like a number you would get no matter where you live — which is exactly the point. If you are ever confused whether a given pressure is station pressure or ESLP, refer to Figure 1 to get the ballpark pressure for the report location. Example: Reported Denver pressure is 998 mb. That has to be ESLP since the typical station pressure at 5,000' is around 850 mb, ± 20 mb. (Note: To use an ESLP in the tools, there is no need to convert it to a station pressure. Think of it as a station pressure at sea level. So enter the ESLP as the station pressure and enter 0' for the station altitude.) The ideal way to use these tools is to have a pressure observation as close as possible to the altitude of interest. This is because the deviation from average conditions can change with altitude. For example, it is possible to have a slightly lower than normal pressure in Manitou but a higher than normal pressure at the top of Pikes Peak. So using info like in Figure 4 is the better way to go. If you plan to use your own barometer (like on a watch), make sure you know your exact altitude when you note the station pressure. Also, you should ensure that the barometer is well calibrated against another accurate barometer. This can be accomplished by using the ESLP in a nearby weather report. Set your barometer to the station pressure computed using the ESLP to SP calculator below. You should repeat this every so often since your barometer can get out whack with all the up and down it must endure. (Note: It is possible to set your barometer to read ESLP but then its reading will only make sense when used at the altitude where it was set. So this is OK for a barometer you hang on your wall but it is not recommended for a watch barometer.)
Atmospheric pressure and its various units of measurement. Why we are lucky Mt Everest (or Pikes Peak) is not in Alaska. Understanding the hydrostatic equation.
About the AuthorBy Matt Carpenterwww.skyrunner.com Tony is a US Air Force meteorologist who started running with the Incline Club in 1999 and soon became the official Incline Club weather forecaster. I remember one time it was very foggy and Tony said (before we started the run from Manitou Springs) we would break out of the fog about 3 switch-backs before Barr Camp. Sure enough about 2 ½ switch-backs from Barr we were running under clear skies. Often he would give the club 4-5 days advance notice of bad weather when most news reports never saw it coming until it was too late if at all. In 2000 the club also adopted the top mile of the Barr Trail. This is dangerous work because of the weather (one hiker was killed by lightning that year) and Tony made us all feel more comfortable by keeping an eye to the sky. His love of mountain weather was contagious and it was an awesome experience to hear him say “see that cloud, in a few minutes it is going to shoot straight up several hundred feet and then we are going to get some snow” and then just sit back and watch it all happen. He moved away from us to pursue a Ph.D. in atmospheric sciences at the University of Washington in Seattle, but hopes to return to CO someday. We all miss him and we will also miss his PPA/M forecasts that gave remarkably accurate temperature predictions at different points along the course depending on the pace you were running. In 1999, after running a 3:19:21 Ascent during a 5:25:12 Marathon Tony set his sights on a sub 5 hour marathon. In 2000 Tony came to 23 of the last 27 Sunday Incline Club long runs and the hard work paid off when he did a 3:06:10 Ascent during a 4:55:21 Marathon! |
|||||||||||||||
Back to Pikes Peak Central